在这篇文章中我们将继续讨论SURF方法和SIFT方法之间的差异,和它们对比起来的优缺点。
SURF用到的处理方法
尺度空间
获取不同尺度的特征点的核心就是构建尺度空间。SIFT采用的方法是,通过高斯滤波迭代和降采样获得不同尺度的图像金字塔,并且通过相邻图像的相减获得DOG差分金字塔,从而在其中寻找特征点。而SURF与之不同,不通过降采样和迭代来改变尺度,而是通过直接放大滤波模板的方式。从原理上来说,放大滤波器尺寸的确能够改变尺度,但是因为图像的物理尺寸没有改变,给后续的计算带来了一定干扰,所以SIFT算法没有采用这种方法。但是,SURF算法全部是基于近似,所以这一问题影响并不严重,为了降低运算量,采用放大模板的方法。
图像金字塔的组内变换
与SIFT类似,SURF也需要构建图像金字塔,也分成一定的组和组内的层。统一起见,之后我们说到滤波器的尺寸L,指的是盒子滤波器的边长。一般上,第一组第一层的图像由原图与\(L=9\)的滤波器卷积获得。而因为滤波器是按区域划分,区域内权值相等的,通过积分图像可以很轻易地获得卷积之后的图像。这一步相比于SIFT算法,极大地提高了运行速度。
而对于每一组的下一张图片,依然由原图获得,不过,这一次的卷积模板的L发生了变化。每一组都有一个\(l_0\),是这一组初始的L的\(l_0=\frac 1 3L\),它称为响应长度。虽然与数学意义无关,但是响应长度在数值上等于模板中每一个区域在区域特征方向上对应的长度。新模板的响应长度每次增加2,这表示,以第一组为例,第一个模板是\(9\times 9\),第二个是\((9/3+2)*3=15 \times 15\),之后是\(21\times 21\),\(27\times 27\)等等。这样保证每次模板的形状不发生改变。
图像金字塔的组间变换
因为对图像不进行降采样处理,这表示可以直接用上一组生成的图像进行下一组的处理。第n+1组的第一张图像即是第n组的第二张图像,之后每次增加的模板尺寸是上一组的两倍。如图:
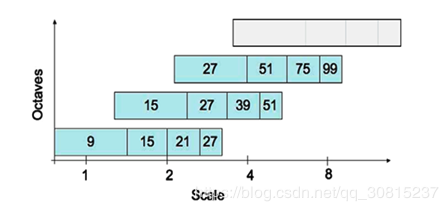
可以看到,首先有很多图使用的模板尺寸是重合的。因为全部是从原图卷积而来,这表示生成的时候可以不用重新生成这些图片,而是直接沿用上一组的图像。其次,因为按照这个速率模板尺寸增加很快,所以不需生成很多图像,一般生成3~4组就可以了。
Hessian行列式图像的生成
在之前的公式中也可以看到,在SURF算法的尺度空间中,每一组中每一层包括三种盒子滤波器,在分别使用三种滤波器之后,可以通过之前文章中描述的加权公式合成Hessian行列式图像。
特征点的获取
特征点的获取与SIFT一致,都是先做差分运算,再在周围26个像素中比较中心像素是否是最大值。而且因为SURF已经使用Hessian矩阵处理图像,无需进行SIFT的边缘响应点排除。同样地,也可以使用阈值处理法来排除低对比度点。
描述子的构建
与SIFT方法一样,为了保证特征矢量具有旋转不变性,需要对每个特征点分配一个主方向。不同的是,因为直方图统计方法太耗费时间,在这里使用Haar小波变换来对特征点邻域进行处理。
什么是Haar小波变换
在讲Haar小波变换之前,我们先来看一下什么是小波变换。如果接触过小波变换,比如在数据挖掘或信号处理之中,可以跳过这里,因为图像处理的小波变换和这些小波变换没有区别。
我们先来看傅里叶变换。傅里叶变换是通过将信号分解成正余弦函数来处理信号,能够将时域信号转换为频域信号(即,变换后的结果不包含或只有很少的类似相位的时间信息,而包含有很丰富的频率信息),方便信号处理。但是它的缺点也很明显,用不会衰减的三角函数作为函数空间的基导致在时间上很不同但是频域上相同的信号将得到非常相似的结果,所以只适合于平稳的信号。基于这个问题,有人提出了短时傅里叶变换,通过窗口扫描来包含时域信号,但是也有自己的缺陷,于是,产生了小波变换。
小波变换和傅里叶变换的最大的区别是,小波变换使用会随时间衰减的小波作为函数空间的基,这样就很好的包含了时域信息。而Haar小波是其中的一种,它的表达式是这样的:
\[\psi (t)=\left\{ \begin{array}{l l}1 & 0\leq t<{1 \over 2}\\ - 1 & {1 \over 2}\leq t<1 \\ 0 & \text {otherwise} \end{array} \right\}\]可以看到,它是具有对称性、有限支撑的正交小波,而且计算简单(总共只有两部份两个系数),但不是连续小波,只有一阶导数,因此有一定限制和精度损失。
小波变换与傅里叶变换类似,但是有一点不同,即它有两个参数,分别是scale和translation。scale描述是小波的收缩,导数是频率,translation控制的则是小波在时间轴上的平移。但是在图像处理中,没有所谓的时间轴(因为我们研究的图像处理不是对视频流而是对帧进行处理,对视频流进行处理的技术如果以后有机会我会展开解释),所以在图像处理中的Haar小波变换依然是用模板进行的卷积。因为我们这里计算的是边缘响应,所以使用边缘响应的Haar模板:

两个模板分别是用来计算x和y方向的Haar小波响应的模板。考虑到其带宽,小波模板的尺寸是\(4s\)。
描述子主方向分配
首先我们约定,对于一个特征点,其尺度是\(s={ { 1.2 \times L } \over 9 }\),这个公式可能看起来奇怪,其实这是为了和高斯卷积尺度保持一致。在计算描述子主方向的时候,以特征点为中心,\(6s\)为半径,60°为张角建立一个扇形区域,在这一扇形区域中求其小波响应的总和\((m_w,\theta_w)\):
\[\begin{array}{c}m_{w}=\sum_wdx+\sum_wdy\\ \theta_w=\arctan \left({\sum_wdx \over \sum_wdy}\right)\end{array}\]之后以0.2的弧度值滑动这一扇形窗口,不断计算其小波响应。找到综合最大的方向,这一方向就是SURF描述子的主方向。与SIFT同理,强度达到峰值80%的方向可以被认为是这个特征点的副方向,可以生成对应的描述子。这样可以提高匹配成功的机率。
特征向量的生成
在SIFT中,使用128维的特征向量来构建描述子,这一操作比较精确,但是比较耗时。SURF构建的则是64维的特征向量,在规模上减小了一半。SURF中,在关键点周围选取一个正方形框,方向为关键点的主方向,边长为20s。将其划分为16个区域(边长为5s),每个区域统计25个尺度像素的水平方向和垂直方向的Haar小波特性,这里的方向均是相对于主方向的。
这里有一个新的概念,就是尺度像素。当然这个概念严格来说并不存在,是我自己造出来的,就是为了描述这个现象。之前说过,因为SURF不使用降采样,导致其图像的尺寸始终不变,但是因为尺度的变化,图像包含的信息在逐渐变模糊,可以被看作是一张更小的图片,经过某种升采样过程被放大了。这时候,一个尺度像素指的就是对应的那个“小图片”上的一个像素,即图像中\(s \times s \)的一个区域。那么一个区域的小波特性怎么获取呢?自然不是每个像素都获取,因为信息在这里有了损失,所以我们寻找损失最小的地方,即每个区域的中心像素进行统计即可。
同时,因为这次我们是在矩形区域内进行处理,而非为了获取一个方向,所以这次获取的小波信息是四个维度:
\[(\sum dx,\sum |dx|,\sum dy,\sum |dy|)\]是将25个尺度像素的特征累加起来获取的结果。那么我们一共获得了\(4 \times 4 \times 4 =64\)维的特征向量。这就是描述子的特征向量,最后还可以进行归一化,加强其关于对比度的不变性。
SURF与SIFT对比总结
SURF与SIFT的差异对比
- SIFT使用高斯卷积核对图像进行处理;而SURF使用对高斯卷积核进行简化之后的盒子滤波器进行处理。
- SIFT使用不断迭代卷积和降采样的方法构建图像金字塔;而SURF使用盒子滤波器与原图卷积,利用积分图像加速运算。
- SIFT使用非极大值抑制先排除低对比度点,再使用Hessian矩阵进行处理排除边缘响应;而SURF使用Hessian矩阵构建图像,所以只需要非极大值抑制即可。
- SIFT使用直方图获取方向信息和描述向量;而SURF使用小波变换来处理这个过程。
- SIFT使用128维描述向量;SURF使用64维描述向量。
SURF与SIFT工作效率的区别
首先最明显的区别就是,SURF明显运行速度比SIFT快很多,因为它几乎在每一个步骤上都进行了简化,也利用了积分图像,可以一次性生成全部的图像金字塔。
也有文献指出,在一些情况下,SURF的匹配效果优于SIFT的效果,因为SURF使用一个区域内的梯度而非一个像素的梯度构建描述子。
但是SURF也有其自身的缺陷,因为它基于近似,多次近似获得的结果可能与SIFT差异很大,这将导致在一些情况下,SURF的工作效果不如SIFT。一个最明显的例子是,因为它的各种模板都是矩形的,所以如果目标进行了45°或者类似的面内旋转(比如135°),这样将大幅降低匹配的可能,因为此时原有的特征点经过旋转可能不再符合特征点标准,或者已经无法与原有特征点匹配。不过因为帧间间隔很短,这一个缺陷可以被补偿。
到这里,SURF方法的基本介绍就结束了。在之后的文章中,我将开始基于SURF的图像拼接方法的学习,若有错误,还望指正。