上一篇文章中，我们讨论了卷积和初始化GSS（高斯尺度空间）的操作和含义，在这片文章中，我们将继续学习SIFT特征的知识。
Credit:
本次学习中所引用的研究来自:
王芳芳，陈华 《动态背景下的视频目标跟踪》，硕士学位论文
怎么求SIFT特征
构建高斯差分尺度空间
什么是降采样和升采样
构建高斯差分尺度空间（DOG）的时候，很关键的一个操作就是降采样和升采样。
-
降采样 通俗的来说，降采样指的是，将一幅图像缩小为原来的几分之一时采用的算法。降采样的过程相对容易，因为直接缩小图像的时候，图像信息是富余的。如果将图像缩小S倍，那么它的长宽高都将缩小到原来的1/S。这表明，原来图像上S*S的一个区域，现在将变为一个像素。那么直接将该窗口内像素的各属性（还记得昨天讲卷积的时候讲到的吗）平均之后合成，赋给新像素就可以。
-
升采样 升采样的操作就复杂一些了。因为，升采样与降采样相反，是将图像放大时采用的算法。但是，对于常规的升采样方法，并不能增加图像包含的信息，这表示图像的信息密度将下降。同时为了保证图像的视觉质量，也为了尽量方便之后对图像的操作，需要尽量使图像指标（比如，灰度）连续，这就对使用的算法有更高的要求。 在SIFT中，对每帧图像只进行一次升采样，结合ZYNQ的PL部分运算能力，使得我可以使用更复杂的算法来进行升采样，来提高后面的运行效果。所以本次学习中，我们重点关注双三次插值法。
双三次插值法升采样
因为双三次插值法考虑到插入像素周围的16个像素，运算比较复杂，下面是它的公式：
首先构造BiCubic函数：
\[W(x)=\left\{\begin{array}{ll}{(a+2)|x|^3-(a+3)|x|^2+1}&{\text{for}|x|\leq 1}\\{a|x|^3-5a|x|^2+8a|x|-4a}&{\text{for}1<|x|<2}\\{0}&{\text{otherwise}}\end{array}\right.\]其中，a取-0.5。对待插值的像素点\((x,y)\)，取其附近的\(4 \times 4 \)邻域点\((x_i,y_j) \text {,i,j=0,1,2,3}\)，按如下公式进行插值计算：
\[f(x,y)=\sum_{i=0}^3 \sum_{j=0}^3 f\left( x_i,y_j \right)W\left( x-x_i\right) W \left(y-y_j\right)\]这个公式的涵义就是：利用三次多项式S(x)求逼近理论上最佳插值函数sin(x)/x，考虑一个像素周围的16个像素，它们的参数对这个像素有权值不等的贡献。W用于计算权值，而最终像素f(x,y)是一个求和的值。仔细看的话会发现这个格式很熟悉，这不就是卷积么？没错，双三次插值法也叫立方卷积插值。
形象一点说，对于目标图像上一点，它在原图上的坐标是(x,y)，因为x和y可能不是整数，所以，用(i,j)表示整数部分，用(u,v)表示小数部分，即目标图像素f(x,y)=f(i+u,j+v)。如图：
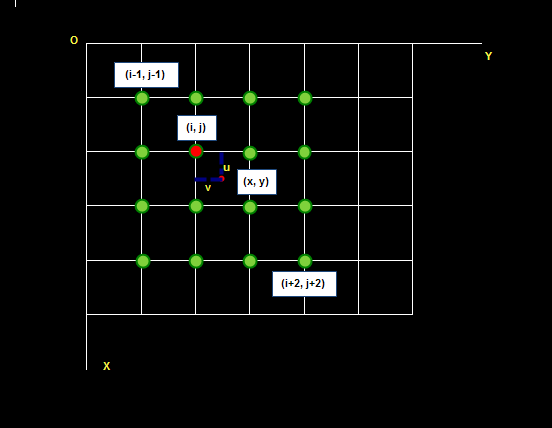所以是16个像素。网上有许多实现双三次插值的算法，在此不一一列举，有一篇代码给的注释比较详细，结构也比较清楚的，可以作为学习例子。
构建高斯金字塔
终于回到了我们的正题上：构建DOG的第一步就是构建高斯金字塔。高斯金字塔严格来说不是一个金字塔，而是一个金字塔组。它由O组S层金字塔构成。每一组组内的图像尺寸是一样的，但是后一幅图片是由上一幅图片经过高斯卷积而来。下一组图象是由这一组图像经过降采样得到，尺寸较上一组图片小一些。
构建高斯金字塔的时候遵循这样的原则。一般情况下，构建的金字塔组数O满足：
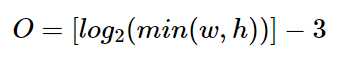其中，(w,h)分别表示图像的宽和高。而每组内图片层数S+3（为什么要+3将在之后讨论）一般设置为6~9层。
那么，我们先从第一组第一层开始说起。首先需要解决的问题是：第一组第一层的图象是什么？要注意，这里的第一张图片并不是原图，而是由原图经过卷积形成的第一张图片。那么原图是什么？Lowe在论文中解释，第1层的尺度建议定为1.6，原图的尺度建议定为0.5，因为取景器，比如相机，一般会做这样一个处理以维持图片质量。这样就带来了一个问题：因为原图是由0.5的平滑器处理过的，相当于一部分信息已经丢失了。这个时候需要引入刚才到的升采样操作，将原图放大为原来的2倍。由这张放大的图片进行卷积生成第一层第一张图片，才能保证最大程度上利用原图信息。同时，因为第一层的尺度是1.6，但是刚才解释过，原图并不是真正的原图，此时进行卷积的图片的尺度应该是2*0.5=1。那么，此时应用在升采样后的图片上的卷积尺度就应该是
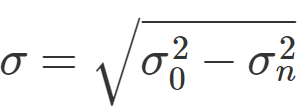用此尺度对升采样后的图片进行卷积，获得第一组第一层。
之后，对于整个第一组而言，就是重复卷积生成每一层。之前也提到，高斯金字塔的形成过程是迭代，而非每次从原图生成，其中有比较复杂的论证关系，在多篇论文中也有研究。但是因为我没看懂与主题无关，在此不展开。因为尺度空间是连续的（感觉更应该说是间隔均匀的，连续一词有歧义，不过因为主流的翻译和教材上都用连续，这里保持一致），这样才能保证对于每一个尺度的特征都没有跳过，所以不能用一样的尺度来进行迭代。每次迭代的尺度应该是两层之间的相对尺度，对于第一组第i和i+1层之间的相对尺度，计算公式是：
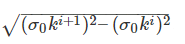其中，σ0是Lawe的建议值，为1.6。而我们也说过，为了保证尺度空间间隔一致，之后也一直沿用这一相对尺度。但是因为每到新的一组，i将被重置，所以作为补偿，需要额外加上一个参数。σ0将被替换成该组的初始尺度，即2^O*σ。
注意：为了统一表示，我们将由升采样卷积获得的图片，即上文的第一组第一层表示为O=0,即索引号为0。
对于尺度空间第o组，第s层的图像，它的尺度为
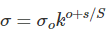这表示，第o组倒数第三幅图像，其尺度与第o+1的第一幅图像一致。那么，取每一组倒数第三幅图像，进行降采样，比例为1/2，可以获得下一组第一幅图象。注意：这里降采样之前不对倒数第三幅图像进行高斯卷积。最终，能够获得一个高斯金字塔。
构建高斯差分尺度空间（DOG）
完成高斯金字塔的构建之后，下一步就是构建高斯差分金字塔。相比较于之前的复杂操作，这一步相对容易很多，高斯差分金字塔与高斯金字塔结构一致，生成过程是用高斯金字塔每一组内的两幅图像差分生成。公式是：
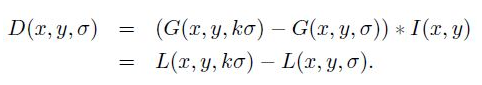其中D(x,y,σ)是最终生成的差分图像。
用这个图可以更形象的展示：
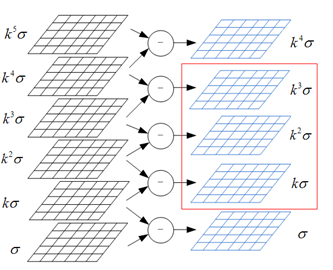可以看到，高斯金字塔的两幅图像差分获得高斯差分金字塔的图像。
研究至此，高斯差分尺度空间的构建就基本完成了。在接下来的文章中，我将继续学习构建完成高斯差分尺度空间之后的SIFT算法，若有错误，还望指正。