在上一篇文章中，我们讲到了寻找并过滤极值点，在本次的学习中，我们将继续关注SIFT特征点提取，重点关注怎样从特征点生成可以匹配的描述子。
怎么求SIFT特征
构建SIFT描述子
确保旋转不变性
所谓的旋转不变性，指的是，对于某一个物体的某种描述特征不随物体旋转而变化。例如，对于人类而言，一个水杯倒过来仍然可以被辨认为一个水杯，这就是人能够识别一些旋转不变的特征。为了确保旋转不变性，我们需要先将描述子主坐标轴旋转至与特征点的方向一致。那么，怎么求特征点的方向呢？
SIFT算法中像素的方向
SIFT算法中，像素的方向被定义为其梯度的方向。计算公式是
\[m(x,y)=\sqrt{(L(x+1,y)-L(x-1,y))^2+(L(x,y+1)-L(x,y-1))^2}\] \[\theta(x,y)={\alpha tan(2{(L(x,y+1)-L(x,y-1))}\over{(L(x+1,y)-L(x-1,y))})}\]其中，\(m(x,y)\)是梯度模长，\(\theta(x,y)\)是梯度的方向。
利用方向直方图判断特征点方向
明白了怎么定义方向之后，需要了解的就是怎样获取特征点的方向。因为特征段虽然是一个点，但是可辨识的特征并非是一个点具有的特征。所以，应该将附近一个区域都包含进来。在以特征点为中心，\(1.5\sigma\)为半径的范围内进行采样，并且将获得的方向信息制成方向直方图。横坐标为方向，45°为一个区间，纵坐标是落在此区间的像素的数量。（有建议和研究认为采用10°一个区间共36区间的算法效果更好，但是这样会加大运算量，也对之后的变换带来不小的麻烦；Lowe也建议此时用高斯函数平滑直方图再进行处理效果会更好，但是同样也会加大运算量。为了达到实时追踪的效果，这两个方案暂且不实施，我准备在完成设计之后，如果ZYNQ还有空闲的计算资源，就尝试修改算法把这两个运算加进去，提高匹配效果）最后，特征点的主方向是最多的方向，对其他达到峰值的80%的方向，标记为这个特征点的次方向。这表示，对于一个有多个峰值的特征点，将产生多个描述子。这些冗余的描述子对完整匹配有很大的帮助。
旋转坐标轴
为了保证旋转不变性，描述子坐标轴方向应该始终与特征点方向保持一致。这样，无论之后特征点如何旋转，因为描述子坐标轴始终匹配，能够最大程度的降低因为平面内旋转带来的改变。这一步用到的公式就是经典的转轴公式：
\[\lbrace_{y=x'sin(\theta)+y'cos(\theta)}^{x=x'cos(\theta)-y'sin(\theta)}\]这一公式是用来进行绕原点旋转的坐标系转换的。
构建128维描述子
取16*16邻域窗口并进行方向运算
以特征点为中心，取16*16像素窗口。16*16的像素窗口可以被分为4*4的16个小区域，而每一个区域被称为一个种子区。在每个种子区内计算方向直方图，计算步骤与上文描述的一致，不同的是：
-
这次操作中，要对每一个像素的方向进行高斯加权处理。如下示意图：
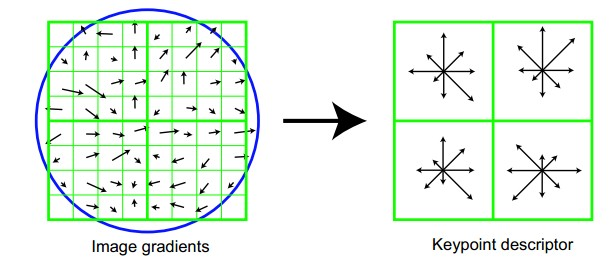如图是4个种子区的加权示意，蓝色的圆圈是加权的范围。最终将形成右侧的种子区。至于加权所用的函数，就是我们这次学习一直在使用的高斯函数。 -
这次不是保留主方向，而是保留全部8个方向，形成\(4\times4\times8=128\)维的矢量。
这一矢量，就是描述子的关键和雏形。
示意图如下：
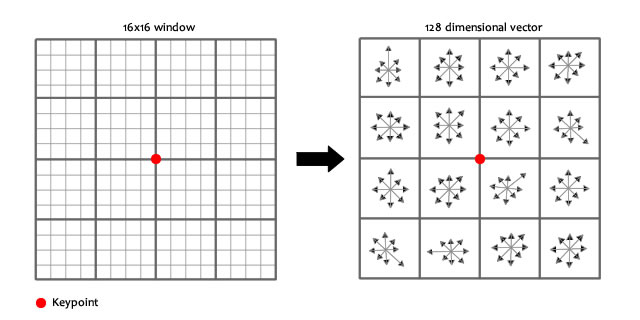
左侧是原始状态，右侧是形成了128维描述子的状态。
归一化
经过前述变换，描述子已经具有尺度不变性和旋转不变性，为了简便之后的操作，需要归一化将每个维度的长度重新映射，以排除因为光照因素带来的干扰。
设定阈值截断描述子梯度
因为非线性光照对某一个方向的梯度有很大的贡献，但是对整体方向贡献微弱，这表示它会带来某一方向梯度值过大的情况。所以，最后的处理中，第一步是对整体描述子维度设定阈值，超过阈值的梯度值将被截断至阈值，从而限制光照影响。这一阈值通常根据经验设定，我将在之后同这方面的学者确认，获得合适的范围。
梯度归一化
因为本次运算虽然产生了矢量，但是本质不是矢量直接参与运算，而是匹配矢量值，所以这里的归一化不是指把矢量转化为标量，而是重映射梯度值到合适的范围，这样能够进一步排除非线性光照的影响。同样的，归一化函数我也将在之后同学者确认。
到了这一步，SIFT描述子的构建就完成了！（终于完成了，折腾了这么久，虽然我的算法还差好多才能实现……）
SIFT匹配
有关SIFT匹配的难度就低了一些，因为整个SIFT算法的核心就是描述子，获得之后的匹配比较常规。
获得欧氏距离
SIFT算法中，两个描述子的相似度是由欧氏距离描述的。高维空间中的欧式距离与简单的欧氏距离一样，指的都是欧氏空间中两点之间的直线距离。计算方法也类似：
\[\sqrt{\sum_{n=0}^{127} {m_n}}\]其中\(m_n\)是第n维方向上的模长。
欧氏距离匹配
在上一帧图像中获取待匹配描述子A，查找下一帧图片中的描述子，找到距离其欧氏距离最近的B和次之的C，其欧氏距离分别为\(d_b\)和\(d_c\)。计算\({d_b}\over{d_c}\)，如果小于一个特定的阈值，则认为A与B匹配。否则，认为A没有匹配点，调节这一阈值可以改变匹配精度，但是阈值越低，精度越高，匹配点也会越少。同样，这一阈值的合适范围我也将与学者求证。
在今天的文章里，我们终于完成了对SIFT方法的初步学习（撒花），在之后的文章中，我将继续学习目标追踪算法，若有错误，还望指正。